Derivate für Anfänger – Teil 3 – Volatilität handeln (Michael Gredenberg)
Volatilität steht für die Schwankungen an den Märkten. (lat. “volare” = fliegen). Sie misst wie stark Kursschwankungen in einem bestimmten Zeitraum sind – also quasi die Turbulenzen am Flug des Marktes.
Volatilität steht für die Turbulenzen am Markt
Aber auch Volatilität selbst kann man handeln, da es eine erwartete Volatilität (=implizite Volatilität) und eine tatsächliche Volatilität gibt (die natürlich noch niemand kennen kann).
Derzeit ist die implizite Volatilität bei vielen Märkten extrem niedrig.
Heute zeige ich, wie man diese Assetklasse “Volatilität” mit Hilfe von Optionen handeln kann.
Dazu werde ich in das Thema “Optionsstrategien” vorstoßen und eine einfache Optionsstrategie zeigen.
Volatilität als Asset-Klasse
Derzeit ist die erwartete (implizite) Volatilität – besonders im amerikanischen Aktienmarkt sehr gering. Volatilität kann auch als Maßstab für Angst gesehen werden. Die Angst vor Turbulenzen am Markt ist gerade nicht sehr groß wie man an der Entwicklung des Volatilitätsindex VIX sehen kann. Es bietet sich also an, auf einen Anstieg der Angst im Markt zu spekulieren oder sich gegen so einen Anstieg der Turbulenzen abzusichern.
Der Volatilitätsindex VIX seit einem Jahr
Neben Anleihen, Aktien, Rohstoffen und Immobilien gilt auch die Volatilität als Anlageklasse (auf englisch: “Asset-Klasse”). Vielen Anlegern ist das sicher nicht bewusst, aber man kann auch Volatilität in sein Portfolio aufnehmen und dadurch die Diversifikation verbessern.
Wie funktioniert das?
In Optionen sind – wie wir bereits im Teil 2 dieser Serie gesehen haben – die erwarteten Kursschwankungen einer Aktie oder eines Indices oder irgendeines anderen Underlyings eingepreist.
Wenn man es nun schafft, alle anderen Risiken die mit einer Option verbunden sind, auszuschalten, so kann man die reine Volatilität handeln.
Kursrisiko ausschalten:
Wie wir in den ersten Teilen der Serie gelernt haben, gibt es Call und Put-Optionen. In beiden Fällen gibt es ein erhebliches Kursrisiko. Kauft man eine Call-Option und diese ist beim Verfall nicht im Geld (Out-of-the-money, OTM) so verfällt die Option wertlos und man verliert seinen gesamten Einsatz. Das passiert wenn der Kurs des Underlyings nicht stark genug steigt oder gar sinkt.
Bei einer Put-Option ist das Gegenteil der Fall: Steigt der Kurs zu stark an, verfällt diese wertlos, da sie ja für ein Underlying einen bestimmten Preis garantiert. Ist der Markpreis aber höher als der garantierte Preis, so bringt die Option nichts und ist wertlos.
Nun gilt es, eine Möglichkeit zu finden dieses Risiko zu eliminieren, man sagt dazu im Fachjargon: “eine delta-neutrale Strategie”. Was das genau bedeutet werde ich in einem weiteren Teil dieser Serie erläutern.
Die Kombination von Call und Put:
Kauft man nun gleichzeitig eine Call-Option und eine Put-Option mit dem selben Ausübungspreis – am besten so nahe wie möglich am Geld, damit sich keine Asymentrie ergibt, so schaltet man das Kursrisiko komplett aus.
Beispiel:
Auf den S&P 500 Index gibt es einen bekannten ETF (exchange traded fund) der diesen Index 1:1 abbildet. Investiert man in diesen ETF so gleicht das quasi einer Investition in den Index.
Dieser ETF (mit dem Börsekürzel SPY) wird derzeit mit 212,99 USD gehandelt.
Eine Call Option mit Verfallsdatum 19.6.2015 und Strike 213 (also so gut wie “am Geld”, “at-the-money”, “ATM”) kostet derzeit USD 2,31
Eine Put-Option mit dem selben Strike und Verfallsdatum kostet USD 2,98
Zusammen kosten diese beiden Optionen also USD 5,29 – das entspricht 2,48% des Preises vom SPY-ETF.
Sinkt der Kurs also vor dem Verfallstag der beiden Optionen um mehr als 2,48% so macht man mit dieser Optionsstrategie einen Gewinn, da der Ertrag den die Put-Option in diesem Fall bringt (Strikt ist ja ATM) die Kosten der beiden gekauften Optionen übersteigt.
Steigt der Kurs vor dem Verfallstag um mehr als 2,48% macht man ebenfalls Gewinn, da in diesem Fall der Ertrag der Call-Option die Kosten der beiden Optionen übersteigt.
Bleibt der Kurs innerhalb einer Bandbreite von -2,48% bis +2,48% macht man Verluste. Ändert sich der Kurs überhaupt nicht d.h. ist er am Verfallstag genauso wie heute, so erleidet man einen Totalverlust, da beide Optionen wertlos verfallen.
Man sieht also: Das Kursrisiko ist bei dieser Strategie weitgehend ausgeschalten: Es ist egal ob der Kurs des Underlyings steigt oder fällt. Wichtig ist nur: Wie stark sind die Schwankungen.
Mit einem “Straddle” hat man also die Möglichkeit in Volatilität zu investieren.
graphische Darstellung:
Um das zu verdeutlichen habe ich einen Chart angefertigt, an dem man sieht, wie die Gewinn/Verlust-Situation in unserem Beispiel aussieht. Auf der X-Achse ist der Kurs des Underlyings (in diesem Fall der ETF SPY auf den Index S&P 500) am Verfallstag der Optionen aufgetragen und auf der Y-Achse der Gewinn bzw. Verlust.
Deutlich zu erkennen ist, dass sowohl bei einem starken Kursanstieg, als auch bei einem starken Kursverlust Gewinne warten. Bleibt der Kurs aber innerhalb einer Bandbreite von ca. 207,5 bis 217,5 so warten Verluste bis hin zum Totalverlust.
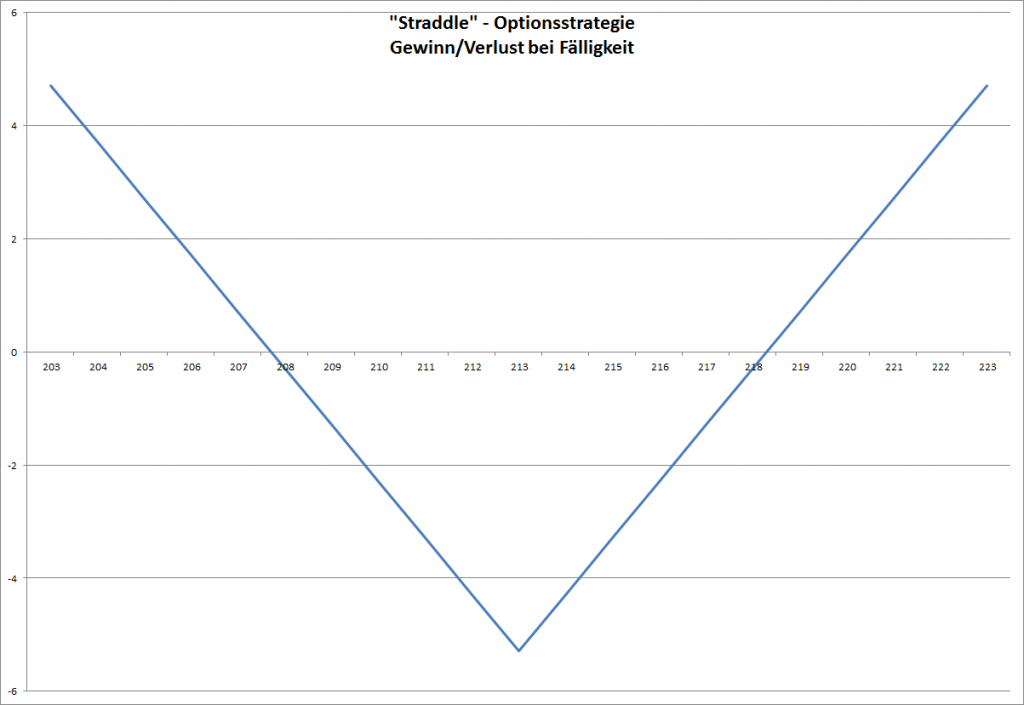 Die Optionsstrategie “Straddle” als Chart
Die Optionsstrategie “Straddle” als Chart
Vega – die Abhänigkeit des Optionspreises von der impliziten Volatilität.
Um die komplexe Entwicklung von Optionspreisen vor dem Verfall verständlicher zu machen, gibt es Kennzahlen, die man “die Griechen” nennt.
Die wichtigsten Vertretet “der Griechen” sind: Delta, Gamma, Theta und Vega.
Heute beschäftigen wir uns vor allem mit Vega – die übrigen Griechen werde ich in späteren Artikeln ausführlich behandeln.
Nun ein kurzer Überblick über die Griechen:
Delta gibt an, um wieviele Punkte sich der Preis einer Option ändert, wenn sich der Preis des Underlyings um einen Punkt ändert.
Gamma gibt an, um wie viel sich Delta ändert, wenn sich der Preis des Underlyings um einen Punkt ändert – es ist also quasi die erste Ableitung von Delta und gibt dessen Steigungsrate an.
Theta gibt an um wie viele Punkte sich der Optionspreis pro Handelstag ändert der vor dem Verfall der Option vergeht. Es ist also ein Masstab für den Zeitwertverlust einer Option
Vega gibt an, wie sich der Optionspreis in Abhängigkeit zur erwarteten (impliziten) Volatilität ändert. Jeder Prozentpunkt den sich die implizite Volatilität ändert, ändert sich der Optionspreis um den Betrag von Vega. Ist also Vega z.B. 0,23 (wie im nächsten Beispiel bei der ersten Call-Option) so steigt der Preis der Option um 0,23 USD wenn die implizite Volatilität um ein Prozent steigt.
Ein Beispiel mit 3 verschiedenen Straddles:
| Verfall | Strike | Prämie | Ticker | Vega | Vega % | |
| Call | 19.06.2015 | 213 | 2,31 | SPY US 06/19/15 C213 | 0,23 | 10,02% |
| Put | 19.06.2015 | 213 | 2,98 | SPY US 06/19/15 P213 | 0,23 | 7,79% |
| Straddle | 19.06.2015 | 213 | 5,29 | 0,46 | 8,76% | |
| Call | 15.01.2016 | 213 | 8,56 | SPY US 01/15/16 C213 | 0,68 | 7,89% |
| Put | 15.01.2016 | 213 | 8,56 | SPY US 01/15/16 C213 | 0,68 | 7,89% |
| Straddle | 213 | 17,12 | 1,36 | 7,89% | ||
| Call | 20.01.2017 | 213 | 15,04 | SPY US 01/20/17 C215 | 1,07 | 7,14% |
| Put | 20.01.2017 | 213 | 15,04 | SPY US 01/20/17 C215 | 1,07 | 7,14% |
| Straddle | 213 | 30,08 | 2,14 | 7,14% |
In der oben stehenden Tabelle habe ich 3 verschiedene Straddles gebildet: Einen wie im ersten Beispiel mit Ablauf am 19.6.2015, einen weiteren der bis zum 15.1.2016 läuft und einen dritten der sogar bis 20.1.2017 läuft. Man sieht, dass der Straddle mit Laufzeit bis 2017 (das sind über eineinhalb Jahre) das sechsfache dessen kostet von dem der nur noch einige Wochen läuft.
Ich habe auch die Kennzahl Vega ausgerechnet: Sie ist natürlich (absolut gesehen) bei dem kürzer laufenden Straddle niedriger als bei den länger laufenden, aber die prozentuelle Veränderung der Optionspreise in Abhängigkeit von der Volatilität ändert sich nicht so stark.
Am Beispiel des Straddles der bis 19.6.2015 läuft sieht man z.B., dass sich der Wert dieses Straddles um 8,76% erhöht, wenn die Angst im Markt (und damit die implizite Volatilität) um 1% steigt.
Rechnet man also kurzfristig mit dem Anstieg von Volatilität so ist es am besten man nimmt Optionen mit kurzer Restlaufzeit – diese sind billiger und man erhält bei einem Anstieg der Volatilität mehr Ertrag, allerdings ist es auch gefährlicher, da dieser Anstieg wirklich rasch erfolgen muss.
Nimmt man Optionen mit längerer Laufzeit so kann man zwar mehr Geduld haben beim Warten auf den Anstieg der Volatiltität, aber man darf nicht vergessen, dass die Option auch einen Zeitwertverlust hat.
Bei Optionen arbeitet man immer gegen die Zeit!
Deshalb ist auch die Kennzahl Theta, die ich bald behandeln werde, sehr wichtig. Jede Option verliert Tag für Tag an Wert – je kürzer die Restlaufzeit ist, umso höher ist dieser Wertverlust.
Möchte man also in die Assetklasse “Volatilität” investieren, so darf man diese Investition niemals als ewig ansehen – so wie z.B. eine Investition in eine Aktie. Man kann es ausnutzen, wenn die Angst (und damit die implizite Volatilität) gerade niedrig ist, sollte aber aussteigen sobald sie wieder hoch ist.
Es gibt keine Buy&hold Strategie für die Investition in Volatilität.
Sollte sich ein Leser meines Blogs aufgrund dieses Artikels dafür interessieren in diese Assetklasse (Volatilität) zu investieren (was ich durchaus für sinnvoll halte) so rate ich dennoch davon ab, das zu tun bevor er sich nicht weiter über Optionen und Optionsstrategien informiert hat. Zumindest sollte er noch einige Wochen warten, bis ich weitere Beiträge zu diesem Thema veröffentlicht habe und sich im Internet oder anderweitig weiter über das Thema Optionen und Optionsstrategien und die damit verbundenen Chancen und Risiken informieren. Das kann sonst in die Hose gehen…
Ich brauche leider noch einige weitere Beiträge um das wirklich interessante Thema der Optionen genauer zu erläutern. Ich hoffe meine Leser werden am Ende ein Gesamtbild davon haben und mit diesem wirklich interessanten Derivat umgehen können.
Straddles mit drei Laufzeiten im Vergleich:
In der nächsten Tabelle zeige ich, wie der Wert von drei verschiedenen Straddles am Verfallstag aussieht.
Links habe ich die Entwicklung des Underlyings (in dem Fall SPY) dargestellt, sowie seine prozentuelle Veränderung am Verfallstag. Im rechten Teil der Tabelle sieht man wie viel % Gewinn oder Verlust man mit einem Straddle macht, wenn man ihn bis zu Verfallstag hält bei entsprechenden Kurs des Underlyings.
Im ersten Fall habe ich als Verfallstag den 19.6.2015 genommen, im zweiten Fall den 15.1.2016 und im dritten Fall den 20.1.2017. (Wie in der vorigen Tabelle)
In der ersten Zeile der Tabelle sieht man z.B. dass, ein Straddle mit Laufzeit bis zum 19.6.2015 einen Gewinn von 486,01% machen würde, wenn der SPY an diesem Tag (im Vergleich zu heute) mit einem Minus von 14,55% schliessen würde.
Auch zu sehen ist, dass im ersten Fall (Laufzeit der Optionen nur ca. 3 1/2 Wochen) eine Veränderung des Underlyings von etwa 2,5% (egal ob Plus oder Minus) ausreicht um in die Gewinnzone zu kommen.
Bei einem Verfall am 15.1.2016 (Reslaufzeit etwas mehr als ein halbes Jahr) müssen es schon 8% Änderung sein (auch egal ob Plus oder Minus) und bei einer Laufzeit bis 20.1.2017 (mehr als eineinhalb Jahre) müssen es über 14% Änderung sein.
Ändert sich aber “unterwegs” – also während der Laufzeit der Optionen – die implizite Volatilität, also wenn die Angst steigt, so kann man die Optionen bereits vor Verfall eventuell mit Gewinn verkaufen.
Der Wertzuwachs der Optionen pro Prozentpunkt Änderung der impliziten Volatilität ist eben Vega.
Und damit es noch ein wenig komplizierter wird: Vega ändert sich natürlich auch ständig – es steigt zum Verfallstag hin an.
| Underlying SPY | Gewinn/Verlust Stradlle in % | |||
| Verfall der Option am | ||||
| SPY bei Verfall | Veränderung SPY % | 19.06.2015 | 15.01.2016 | 20.01.2017 |
| 182 | -14,55% | 486,01% | 81,07% | 3,06% |
| 183 | -14,08% | 467,11% | 75,23% | -0,27% |
| 184 | -13,62% | 448,20% | 69,39% | -3,59% |
| 185 | -13,15% | 429,30% | 63,55% | -6,91% |
| 186 | -12,68% | 410,40% | 57,71% | -10,24% |
| 187 | -12,21% | 391,49% | 51,87% | -13,56% |
| 188 | -11,74% | 372,59% | 46,03% | -16,89% |
| 189 | -11,27% | 353,69% | 40,19% | -20,21% |
| 190 | -10,80% | 334,78% | 34,35% | -23,54% |
| 191 | -10,33% | 315,88% | 28,50% | -26,86% |
| 192 | -9,86% | 296,98% | 22,66% | -30,19% |
| 193 | -9,39% | 278,07% | 16,82% | -33,51% |
| 194 | -8,92% | 259,17% | 10,98% | -36,84% |
| 195 | -8,45% | 240,26% | 5,14% | -40,16% |
| 196 | -7,98% | 221,36% | -0,70% | -43,48% |
| 197 | -7,51% | 202,46% | -6,54% | -46,81% |
| 198 | -7,04% | 183,55% | -12,38% | -50,13% |
| 199 | -6,57% | 164,65% | -18,22% | -53,46% |
| 200 | -6,10% | 145,75% | -24,07% | -56,78% |
| 201 | -5,63% | 126,84% | -29,91% | -60,11% |
| 202 | -5,16% | 107,94% | -35,75% | -63,43% |
| 203 | -4,69% | 89,04% | -41,59% | -66,76% |
| 204 | -4,22% | 70,13% | -47,43% | -70,08% |
| 205 | -3,75% | 51,23% | -53,27% | -73,40% |
| 206 | -3,28% | 32,33% | -59,11% | -76,73% |
| 207 | -2,81% | 13,42% | -64,95% | -80,05% |
| 208 | -2,34% | -5,48% | -70,79% | -83,38% |
| 209 | -1,87% | -24,39% | -76,64% | -86,70% |
| 210 | -1,40% | -43,29% | -82,48% | -90,03% |
| 211 | -0,93% | -62,19% | -88,32% | -93,35% |
| 212 | -0,46% | -81,10% | -94,16% | -96,68% |
| 213 | 0,00% | -100,00% | -100,00% | -100,00% |
| 214 | 0,47% | -81,10% | -94,16% | -96,68% |
| 215 | 0,94% | -62,19% | -88,32% | -93,35% |
| 216 | 1,41% | -43,29% | -82,48% | -90,03% |
| 217 | 1,88% | -24,39% | -76,64% | -86,70% |
| 218 | 2,35% | -5,48% | -70,79% | -83,38% |
| 219 | 2,82% | 13,42% | -64,95% | -80,05% |
| 220 | 3,29% | 32,33% | -59,11% | -76,73% |
| 221 | 3,76% | 51,23% | -53,27% | -73,40% |
| 222 | 4,23% | 70,13% | -47,43% | -70,08% |
| 223 | 4,70% | 89,04% | -41,59% | -66,76% |
| 224 | 5,16% | 107,94% | -35,75% | -63,43% |
| 225 | 5,63% | 126,84% | -29,91% | -60,11% |
| 226 | 6,10% | 145,75% | -24,07% | -56,78% |
| 227 | 6,57% | 164,65% | -18,22% | -53,46% |
| 228 | 7,04% | 183,55% | -12,38% | -50,13% |
| 229 | 7,51% | 202,46% | -6,54% | -46,81% |
| 230 | 7,98% | 221,36% | -0,70% | -43,48% |
| 231 | 8,45% | 240,26% | 5,14% | -40,16% |
| 232 | 8,92% | 259,17% | 10,98% | -36,84% |
| 233 | 9,39% | 278,07% | 16,82% | -33,51% |
| 234 | 9,86% | 296,98% | 22,66% | -30,19% |
| 235 | 10,33% | 315,88% | 28,50% | -26,86% |
| 236 | 10,80% | 334,78% | 34,35% | -23,54% |
| 237 | 11,27% | 353,69% | 40,19% | -20,21% |
| 238 | 11,74% | 372,59% | 46,03% | -16,89% |
| 239 | 12,21% | 391,49% | 51,87% | -13,56% |
| 240 | 12,68% | 410,40% | 57,71% | -10,24% |
| 241 | 13,15% | 429,30% | 63,55% | -6,91% |
| 242 | 13,62% | 448,20% | 69,39% | -3,59% |
| 243 | 14,08% | 467,11% | 75,23% | -0,27% |
| 244 | 14,55% | 486,01% | 81,07% | 3,06% |
| 245 | 15,02% | 504,91% | 86,92% | 6,38% |
Der Beitrag Derivate für Anfänger – Teil 3 – Volatilität handeln erschien zuerst auf Financeblog.
Latest Blogs
» SportWoche Podcast #155: Lili Tagger und A...
» Börse-Inputs auf Spotify zu u.a. Ex-Börseh...
» Österreich-Depots: Irre Weekend Bilanz, ab...
» Börsegeschichte 4.4.: Das wird wohl einer ...
» Nachlese: Danke Sophie Wotschke, Rudi Grei...
» Wiener Börse Party #877: Grösster ATX TR-P...
» PIR-News: Pierer Mobility, AMAG, BKS Bank,...
» 618 intraday vs. 605 (Christian Drastil)
» Börse-Inputs auf Spotify zu u.a. gettex-Po...
» Börsepeople im Podcast S18/08: Max Pohanka
Michael Gredenberg

Inode-Gründer. Heute u.a. passionierter Radfahrer und Finanzautor via financeblog.at.
Weitere Blogs von Michael Gredenberg
» Apple - Wird der Apfel faul? (Michael Gred...
Apple hat letzte Woche mit der Veröffentlichung der Ergebnisse des letzten Quartals (Fisk...
» Unternehmensgründer vs Manager - welche Ak...
Einige der größten Konzerneder Welt werden heute noch von ihren Gründern geleite...
» Tesla - eine Bewertung unter neuen Gesicht...
Tesla – der innovative Elektroautohersteller aus dem Silicon Valley – hat letzte W...
» Negative Zinsen - an Aktien führt kein Weg...
Letzten Donnerstag hat die EZB mit der Senkung des Leitzinssatzes im EUR-Raum auf Null sowie der...
» Korrelation und Kausalität (Michael Greden...
Korrelation misst den Zusammenhang zwischen mehreren Ereignissen wie z.B. auch der Entwicklung v...