Derivate für Anfänger â Teil 2 â Bewertung von Optionen (Michael Gredenberg)
Im ersten Teil der Derivate-Serie habe ich die Funktionsweise von Optionen erklärt.
Heute gehe ich einen Schritt weiter und möchte erklären, wie man Optionen bewertet.
Ich werde außerdem aufzeigen, dass das eigentlich unmöglich ist und welche fatale Folgen diese Tatsache in der Vergangenheit schon hatte.
Soviel vorweg: Dieses Thema ist recht komplex, und deshalb ist das bisher der längste Artikel im Financeblog. Ich hoffe es gibt dennoch einige interessierte Leser die ihn bis zum Ende lesen.
Es geht los:
Die Bewertung einer Option am Fälligkeitstag haben wir ja bereits im letzten Teil gelernt – und die ist relativ einfach.
Noch einmal zur Wiederholung am Beispiel einer Call-Option: Wir erinnern uns: Eine Call-Option (auch Kauf-Option genannt) auf eine bestimmte Aktie (Underlying) berechtigt an einem festgelegtenZeitpunkt (dem Fälligkeitstag) zum Kauf dieser Aktie zu einem festgelegten Preis (auch “Strike” genannt).
Der Wert der Call Option am Fälligkeitstag ist also einfach zu berechnen : Kurs des Underlyings am Fälligkeitstag minus Strike-Preis
Ein Beispiel: Eine Call-Option auf die Aktie X (=Underlying) hat den Strike 100 und die Fälligkeit am 20. Februar 2015.
Sollte die Aktie X am 20. Februar 120 kosten, so ist die Call-Option 20 wert, da man bei Ausübung der Option die Aktie für 100 kaufen und sofort danach für 120 verkaufen könnte.
Wie stellt man den Wert einer Option vor dem Fälligkeitstag fest?
Das ist eine sehr komplexe Frage für deren (vermeintliche) Lösung sogar ein Nobelpreis verliehen wurde: Robert Merton und Myron S. Scholes erhielten 1997 den Wirtschaftsnobelpreis für die Entwicklung des Black & Scholes Modells zur Berechnung von Optionswerten.
Weshalb diese Black & Scholes Formel so komplex ist, und wieso sie dennoch an den realen Finanzmärkten schon oft kläglich versagte möchte ich jetzt zeigen:
Was beeinflusst den Wert einer Option vor dem Verfallsdatum?
Folgende wichtigen Feststellungen müssen wir hierfür treffen:
1) Wenn die Option “im Geld” ist, also der Ausübungspreis (Strike) unterhalb des aktuellen Kurses des Underlyings liegt, so ist die Option MINDESTENS so viel wert wie die Differenz zwischen Kurs des Underlyings und Ausübungspreis.
Die Erklärung dafür, warum das so ist ist recht einfach: Am Fälligkeitstag – wie wir ja eben gesehen haben – ist der Wert der Call-Option genau die Differenz zwischen Kurs des Underlyings und Ausübungspreis (Strike) . Notiert das Underlying bereits vor dem Fälligkeitstag über dem Strike so besteht ja die Chance, dass das Underlying noch weiter steigt und der Optionswert ebenfalls.
Nun kann natürlich das Argument gebracht werden, dass das Underlying ja auch wieder unter den Strike der Option fallen könnte bevor die Option fällig wird. Dagegen kann man sich aber problemlos absichern, indem man das Underlying einfach (Leer)verkauft Am Fälligkeitstag kann man es ja auf jedenfall zum Strike-Preis wieder kaufen und hat die Differenz zum Strike verdient.
Beispiel: Eine Option auf eine Aktie hat den Strike 100 und eine Restlaufzeit von 1 Monat. Die Aktie steht am Bewertungsstichtag – also 1 Monat vor Fälligkeit der Option – auf 120. Man kann diese Aktie also um 120 verkaufen (das geht auch ohne sie zu besitzen, indem man sie sich ausborgt und einfach 1 Monat später zurückgibt – so etwas nennt man Leerverkauf. Über die meisten Online-Broker geht das sehr einfach)
Sollte die Aktie bis zum Fälligkeitstag unter 100 fallen, so verfällt zwar die Option wertlos, aber man kann die Aktie dann billiger zurückkaufen und zurückgeben. Man hat also einen Gewinn von mindestens 20 gemacht.
Sollte die Aktie aber weiter steigen, so übt man am Verfallstag einfach die Option aus, kauft die Aktie für 100 und gibt sie zurück. Da man sie für 120 verkauft hat, hat man einen Gewinn von 20 gemacht – genau die Differenz zwischen Ausübungspreis und Aktienkurs zum Zeitpunkt des Bewertungsstichtages.
Es ist also sinnlos eine Option (auch wenn das bei amerikanischen Optionen erlaubt ist) vorzeitig auszuüben.
2) Der Wert einer Option ist umso höher, je höher die erwarteten Kursschwankungen des Underlyings in der Restlaufzeit sind – dieser Fakt ist der wichtigste bei der Bewertung von Optionen.
Auch diese Tatsache ist recht einfach zu erklären: Schwankt der Kurs des Underlyings stärker so ist die zukünftige Kursentwicklung unklarer und die Gewinnchancen am Fälligkeitstag steigen.
Bzw. anders ausgedrückt: Hätte man statt der Option das Underlying im Portfolio, so wäre man dem kompletten Risiko der Kursschwankungen ausgesetzt – man könnte zwar eventuell viel gewinnen, aber auch sehr viel verlieren. Da eine Option wesentlich weniger Kapital bindet als der Besitz des Underlyings, aber die gleichen Chancen bei der richtigen Kursentwicklung bietet wie eben der Besitz dieses Underlyings (bei einer Call-Option im Falle von steigenden Kursen) muss sich diese Tatsache ebenfalls in der Bewertung der Option widerspiegeln.
Auch hier ein Beispiel zum Verständnis:
Wieder haben wir eine Call-Option auf eine Aktie X mit Strike 100 und Restlaufzeit in diesem Beispiel von einem Jahr. Außerdem haben wir noch eine weitere Call-Option auf Aktie Y, ebenfalls mit Strike 100 und mit der selben Restlaufzeit ebenfalls von einem Jahr.
Aktie X hat eine erwartete Schwankungsbandbreite (Volatilität) von 50% im Jahr. Aktie Y hingegen hat nur eine erwartete Volatilität von 15% im Jahr. Beide Aktien notieren derzeit (am Bewertungsstichtag der Option) bei etwa 100. Beide Optionen sind also gerade am Geld “at-the-money”.
Der Markt erwartet aber im ersten Fall bei Aktie X Schwankungen im nächsten Jahr von 50%, d.h. die Aktie könnte am Verfallstag entweder bei 150 oder bei 66,67 stehen, oder irgendwo dazwischen.
Bei Aktie Y erwartet der Markt nur Schwankungen von 15%, die Aktie könnte also am Verfallstag bei 115 oder bei 86,96 stehen oder irgendwo dazwischen.
Im besten Fall könnte man also bei der ersten Option am Verfallstag einen Wert von 50 realisieren, bei der zweiten Option nur einen Wert von 15. Der Einfluss der Volatilität auf den Wert einer Option ist also sehr hoch.
3) Der Wert einer Option enthält alle Finanzierungskosten bis zum Strike-Preis für das Underlying bis zur Fälligkeit.
Diese Aussage ist am schwierigsten zu verstehen bzw. zu erklären:
Ich fange deshalb hier mit einem Beispiel an:
Aktie X steht derzeit bei 120. Eine Call-Option auf Aktie X mit dem Strike 100 und Laufzeit von einem Jahr kostet also – wie wir gesehen haben – mindestens 20.
Wenn man nun eine Aktie kaufen möchte, muss man 120 investieren. Für den Kauf der Option nur etwas über 20. Kauft man also die Option so muss man also deutlich weniger Kapital aufbringen als der Aktien-Käufer, nimmt aber genauso an Kursgewinnen teil wie ein Besitzer der Aktie.
Der Aktienbesitzer musste sich aber entweder die 120 die er für die Aktie bezahlt hat ausborgen und dafür Zinsen zahlen, oder er hat das Geld am Konto und verzichtet beim Aktienkauf auf Zinsen die er bekäme, hätte die Aktie nicht gekauft sondern das Geld einfach liegen lassen (das nennt man Opportunitätskosten) .
In unserem Beispiel sieht man, dass der Optionskäufer um fast 100 weniger an Kapital aufbringen musste als der Aktienkäufer. Und, da er diese 100 quasi “sparen” kann – also Zinsen dafür einnehmen kann – muss er diese Zinsen auch mit dem Optionspreis bezahlen.
Auf der anderen Seite kann es sein, dass ein Unternehmen noch vor Fälligkeit der Option Dividenden ausschüttet, die höher sind als die Zinsen die für die Finanzierung des Aktienkaufs zu zahlen wären. Diese Dividenden bekommt natürlich ein Optionsbesitzer nicht, da er die Aktie ja erst am Fälligkeitstag erwerben kann, und erst ab dann Anrecht auf Dividendenzahlungen hat.
Deshalb werden erwartete Dividendenzahlungen von dem Wert der Option wieder abgezogen.
Die Finanzierungskosten setzten sich also wie folgt zusammen:
Zinsen für das aufgebrachte Kapital (bis zum Strike) abzüglich der erwarteten Dividenden.
Diese Finanzierungskosten sind immer Teil des Optionspreises (der Optionsprämie)
Nun haben wir also 3 Faktoren ausgemacht, die den Preis einer Option vor Fälligkeit bestimmen:
1) Abstand zum Strike
2) Die Höhe der erwarteten Kursschwankungen (die sogenannte implizite Volatilität)
3) Die Finanzierungskosten
Die Faktoren 1) und 3) sind relativ leicht zu bestimmen und lassen auch nicht viel Betrachtungsspielraum zu. Einzig bei den Zinsen und den erwarteten Dividenden kann es eventuell Ungewissheiten geben, aber die sind bei weitem nicht so groß wie der Hauptfaktor, der die Optionsprämie am meisten beeinflusst: Die implizite Volatilität.
Und genau hier kommt die Nobelpreis-Formel ins Spiel:
Die berühmte Black&Scholes Formel zur Optionsbewertung vergleicht die Kapitalmärkte mit den Zufallsprozessen der brownschen Bewegung. Diese brownsche Bewegung ist eine zufällige Bewegung von Teilchen die in Flüssigkeiten oder Gasen bedingt durch Abstoßungsreaktionen auf andere Teilchen beobachtet werden können.
Eine Grund-Voraussetzung für die Richtigkeit dieser Formel ist die Annahme, dass Kursschwankungen der Finanzmärkte sich völlig zufällig und normalverteilt bewegen.
Normalverteilt bedeutet, dass die einzelnen Kursschwankungen einer Gaußschen Glockenkurve entsprechen. D.h. betrachtet man z.B. ein Jahr mit etwa 260 Handelstagen so wird an den meisten Tagen die Schwankung eher geringer ausfallen. An einigen wenigen Tagen gibt es stärkere Schwankungen.
Kurzer Exkurs: Normalverteilung und Volatilität:
Der Normalverteilung begegnet man beispielsweise, wenn man eine Gruppe von Menschen auf ihre Größe untersucht. Die meisten werden eine Durchschnittsgrösse haben bzw. etwa größer oder etwas kleiner als der Durchschnitt sein. Eine wenige werden extrem klein sein und ebenfalls wenige werden extrem groß. Trägt man die Größen dieser Menschen auf einer Skala auf, wo die X-Achse für die Größe steht und die Y-Achse für die Anzahl der Menschen mit dieser Größe, so erhält man eine Glockenkurve die der Normalverteilung entspricht.
Die Größe der meisten Menschen weicht also nicht sehr stark vom Durchschnitt ab. Je größer die Abweichung vom Durchschnitt, umso weniger Menschen mit ensprechender Größe gibt es. Ganz wenige werden zu Riesen oder bleiben Zwerge – sie sind am Rand der Glockenkurve zu finden.
Die Durchschnittsgröße der Menschen entspricht dem sogenannten Erwartungswert.
Nun haben aber natürlich nicht alle Menschen Durchschnittsgröße. Die meisten sind ein wenig größer oder ein wenig kleiner als der Durchschnitt. Einige wenige sind aber extrem groß (“Riesen”) oder sehr klein (“Zwerge”. Hierbei handelt es sich um sogenannte “Ausreißer”
Rechnet man den durchschnittlichen Abstand der Größen aller untersuchter Menschen zum Erwartungswert aus (also inkl. der Ausreißer) so bekommt man die Standardabweichung.
Die durchschnittliche Abweichung vom Erwartungswert nennt man also Standardabweichung. Untersucht man z.B. 200 Menschen auf Ihre Größe und ermittelt als Durchschnittsgröße dieser Menschen 165cm so sind diese 165cm der Erwartungswert. Der durchschnittliche Abstand zum Erwartungswert ist dann die Standardabweichung. Nehmen wir eine Standardabweichung von 20cm in diesem Beispiel, würde das bedeuten, dass die 200 Menschen im Durchschnitt zwischen 145cm und 185cm gross sind. 68,27% der untersuchten Menschen werden sich in diesem Beispiel innerhalb der Bandbreite +/- 1 Standardabweichung befinden.
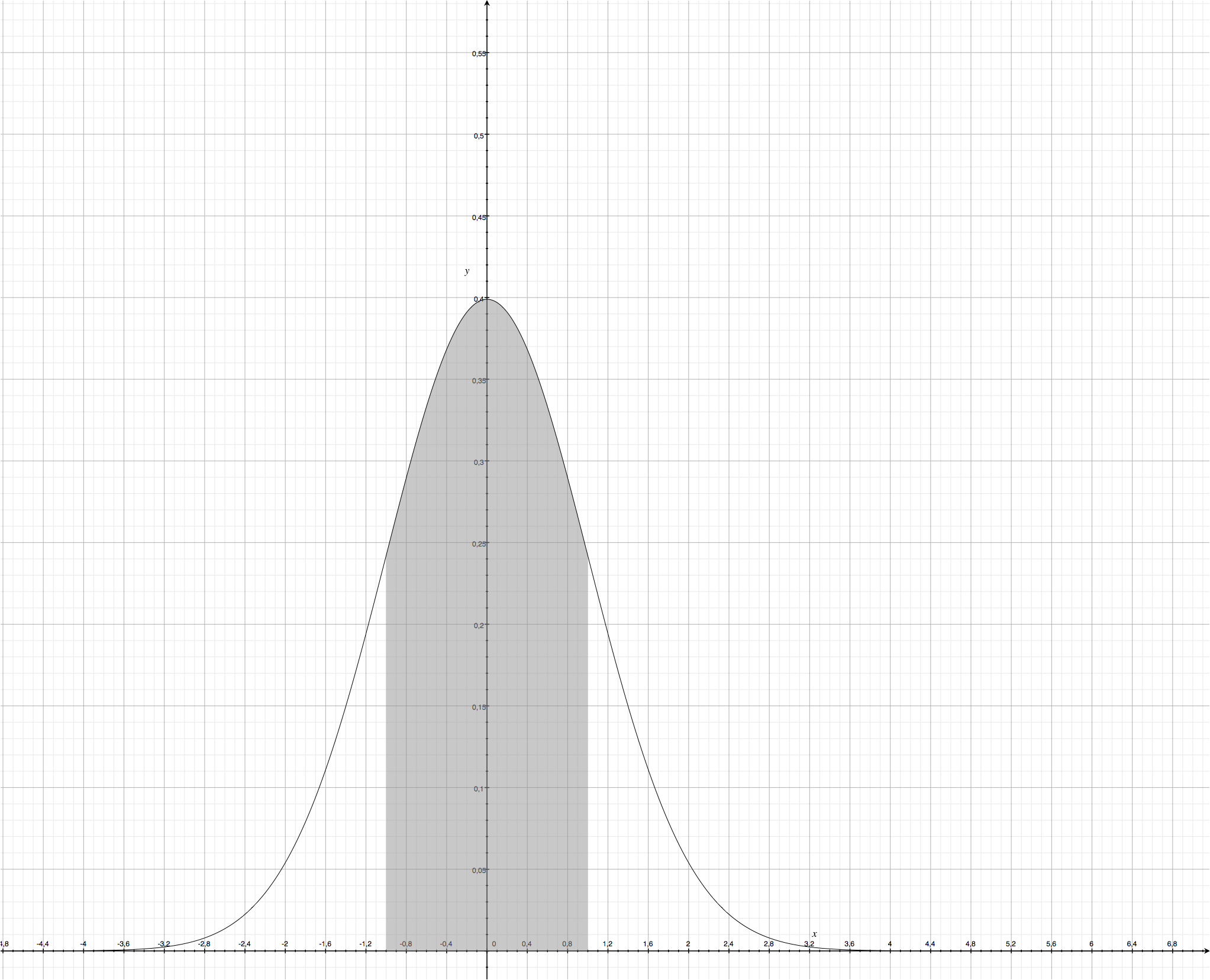
In der Grafik habe ich die Kurve der sogenannten “Standard-Normalverteilung” gezeichnet (mittels dem mit MacOS X mitgelieferten Programm “Grapher” – übrigens ein Juwel für jeden Mathematik-Nerd ![]() )
)
Bei der Standard-Normalverteilung entspricht der Erwartungswert 0 und die Standardabweichung 1.
Ich habe grau den Bereich zwischen einer Standardabweichung hervorgehoben. Für Mathematik-Nerds: Ich habe die Kurve im Bereich -1 bis 1 integriert, also die Fläche darunter ausgerechnet und hervorgehoben.
Die Fläche unter der gesamten Kurve beträgt natürlich 1, da alle möglichen Ereignisse (in unserem Beispiel Körpergrössen) unter dieser Kurve abgebildet sind. Die Fläche zwischen -1 und 1, also innerhalb einer Standardabweichung (auch 1 Sigma genannt), entspricht 0,6827 – d.h. dass eben 68,27% aller Ereignisse (Körpergrößen in unserem Fall) innerhalb von einer Standardabweichung liegen.
Erweitert man die Betrachtung auf 2 Standardabweichungen (2 Sigma) so sind bereits 95,45% aller Ereignisse innerhalb der Kurve.
Nur noch jedes ca. 22te Ereignis wäre außerhalb. In unserem Fall würde das bedeuten, dass nur jeder 22te entweder 165cm + 2 x 20cm = 205 cm gross oder 165cm – 2 x 20cm = 125cm klein wäre. Woran man sieht, dass die Standardabweichung bei Körpergrössen wahrscheinlich kleiner als 20cm ist, da weniger als jeder 20te über 2 Meter groß ist ![]()
Bei 3 Sigma sind es schon 99,73% die sich innerhalb des Bereiches befinden und nur noch jedes 370te Ereignis ist außerhalb.
Bei 4 Sigma sind es 99,993% und jedes 15.787te Ereignis ist außerhalb
Bei 5 Sigma sind es 99,99994% innerhalb und jedes 1.74 Millionste Ereignis ist außerhalb.
Bei 6 Sigma sind es 99,9999998% innerhalb und nur noch jedes 506,8 Millionste Ereignis ist außerhalb.
Man spricht deshalb öfters bei vollkommen unmöglichen Ereignissen an den Märkten die plötzlich dennoch auftraten von “Sigma-6-Events”.
Die Wahrscheinlichkeit, dass ein solcher Event eintritt liegt bei 1 : 507.797.346 . Geht man von etwa 260 Handelstagen im Jahr aus, würde also nur etwa alle 1,9 Millionen Jahre ein derartiger Event eintreten.
Das ist bereits ein erster Hinweis dafür, dass die Normalverteilung nicht einfach auf Finanzmärkte angewandt werden kann.
Normalverteilung auf den Finanzmärkten:
Um zu verdeutlichen wie man sich die Normalverteilung von Renditen (=Kursausschläge) an Finazmärkten erklärt bringe ich nun Beispiele:
Zuerst schauen wir uns die Entwicklung einer Aktie mit geringer Volatilität an: Procter und Gamble hatte im letzten Jahr eine Volatilität von etwa 13%.
Wir betrachten jeden einzelnen Handelstag im letzten Jahr und schauen wie viel die Aktie sich an diesem jeweiligen einen Tag bewegt hat. Diese Bewegungen fassen wir in Abständen von 0,4% zusammen und zählen sie ab.
So hat sich die P&G-Aktie im letzten Jahr am häufigsten zwischen -0,4% und 0% pro Tag bewegt (66 mal) und ebenso oft zwischen 0% un 0,4%. Bewegungen zwischen -3,6% und -3,2% gab es nur ein einziges Mal.
| Kursentwicklung | Anzahl Tage |
| -4,00% | 0,00 |
| -3,60% | 1,00 |
| -3,20% | 0,00 |
| -2,80% | 0,00 |
| -2,40% | 0,00 |
| -2,00% | 5,00 |
| -1,60% | 9,00 |
| -1,20% | 18,00 |
| -0,80% | 37,00 |
| -0,40% | 66,00 |
| 0,00% | 66,00 |
| 0,40% | 35,00 |
| 0,80% | 27,00 |
| 1,20% | 10,00 |
| 1,60% | 3,00 |
| 2,00% | 3,00 |
| 2,40% | 0,00 |
| 2,80% | 1,00 |
| 3,20% | 0,00 |
| 3,60% | 0,00 |
| 4,00% | 0,00 |
| 4,40% | 0,00 |
Grafisch schaut die Tabelle dann so aus:
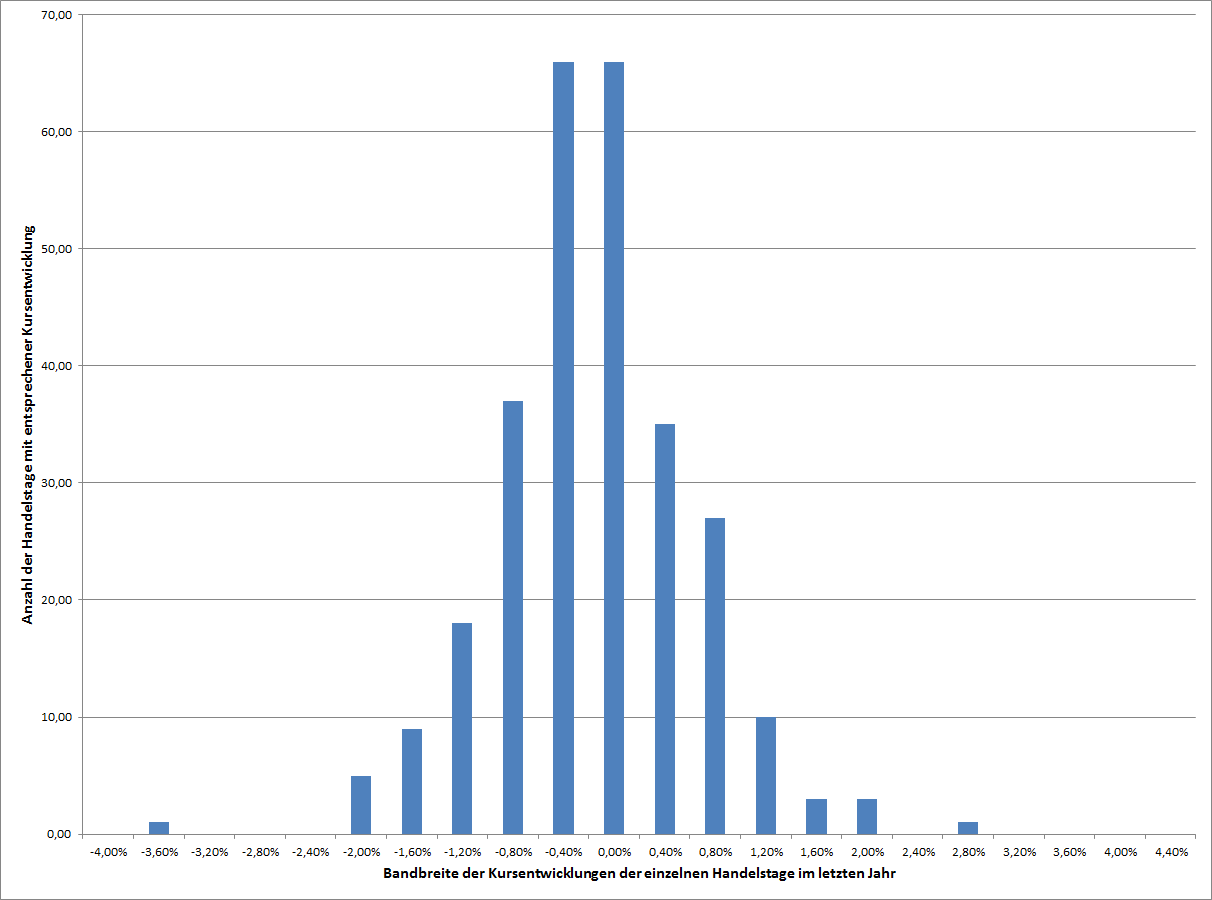 Die Verteilung der Kursschwankungen bei Procter und Gamble im letzten Jahr
Die Verteilung der Kursschwankungen bei Procter und Gamble im letzten Jahr
Wir sehen deutlich eine Häufung in der Mitte die nach links und rechts jeweils nachlässt. Es besteht also eine gewisse Ähnlichkeit mit der Gaußschen Glockenkurve die die Häufigkeit bei einer Normalverteilung beschreibt.
Den Wert, der am aller häufigsten vorkommt – und gleichzeitig auch der Durchschnitt aller Werte – ist der Erwartungswert. In diesem Fall ist das 0,04%. Bei der Normalverteilung streuen sich alle anderen Ereignisse symetrisch um diesen Erwartungswert. Ihre Häufigkeit nimmt mit der Entfernung zum Erwartungswert stetig ab.
Die durchschnittliche Entfernung zum Erwartungswert ist die Standardabweichung. In diesem Beispiel ist die Standardabweichung 0,78%, das bedeutet, dass die durchschnittliche tägliche Kursschwankung bei P&G im letzten Jahr 0,78% um den Erwartungswert von 0,04% war – also zwischen -0,74% (= -0,78 + 0,04) und 0,82% (= 0,78 + 0,04).
Die Standardabweichung ist im Prinzip das was wir in den Finanzmärkten Volatilität nennen. Für die Berechnung Volatilität wird einfach die Standardabweichung der Kursschwankungen der einzelnen Tage annualisiert, d.h. aufs Jahr hochgerechnet. Das geht indem man die Standardabweichung mit der Wurzel aus der Anzahl der Handelstage multipliziert. In diesem Fall erhält man 13,03%. Hierbei handelt es sich um die sogenannte historische Volatilität, da ja die Vergangenheit untersucht wird.
Wir können aufgrund der Regeln die wir oben bereits bei der Normalverteilung gesehen haben also – theoretisch – folgende Schlüsse ziehen:
– In 68,37% der Fälle sollte sich der Kurs zwischen -0,74% und 0,82% (= eine Standardabweichung Abstand vom Erwartungswert bzw. 1 Sigma) bewegt haben
– In 99,994% der Fällen sollte sich der Kurs zwischen -3,08% und 3,16% an einem Tag bewegt haben. Also nur einmal in etwa 15.800 Tagen sollte seine Bewegung außerhalb dieser Bandbreite liegen. Das wäre etwa alle 61 Jahre einmal an einem Tag der Fall.
Dennoch sehen wir, dass es einen Tag gibt, wo der Kurs zwischen 4% und 3,6% verloren hat, also mehr als 3,08%.
An diesem Beispiel ist zu erkennen, dass die Kursschwankungen an den Finanzmärkten nicht hinreichend durch die Normalverteilung erklärbar sind.
Es gab im letzten Jahr sogar (mindestens) eine Aktie die es geschafft hat mehr als ein “Sigma-6-Ereignis” zu erreichen, also etwas, das seltener als einmal in 1,9 Millionen Jahren passieren dürfte:
Im nächsten Bild habe ich die täglichen Kursschwankungen der Aktie “First Solar” als Diagramm dargestellt.
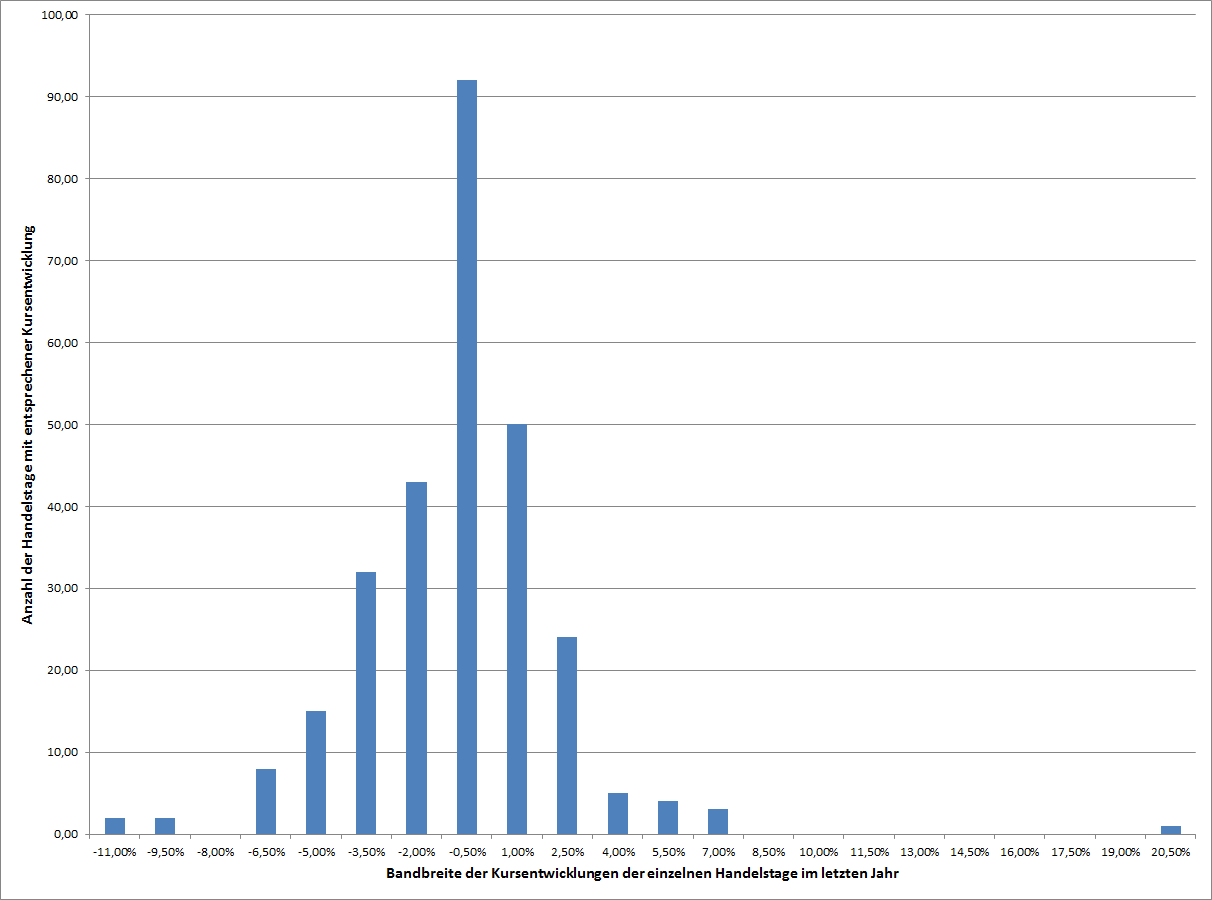 Die Verteilung der Kursschwankungen von First Solar im letzten Jahr
Die Verteilung der Kursschwankungen von First Solar im letzten Jahr
Auf den ersten Blick schaut das auch ein wenig nach Glockenkurve und Normalverteilung aus. Der Erwartungswert liegt hier bei -0,01%, Die Standardabweichung bei 2,99% (also bereits wesentlich höher als bei Procter and Gamble) und die annualisierte Volatilität beträgt 50,07%.
Aber eine Auffälligkeit gibt es: An einem Tag stieg die Aktie um 20,5%. Das entspricht einen Abstand von sagenhaften 6,88 Standardabweichungen. Die Wahrscheinlichkeit, daß das eintritt liegt bei etwa 1 zu 100 Milliarden. Es sollte also nur etwa alle 384 Millionen Jahre passieren. Also jedenfalls nicht ein einziges Mal seit Menschengedenken. Vor 384 Millionen Jahren bevölkerten noch Einzeller die Erde.
Zurück zur Black & Scholes Formel:
Der wichtigste Kniff bei der Black & Scholes Formel war es eben diese Normalverteilung auf die Finanzmärkte anzuwenden.
Die Annahme war, dass sich die Kursschwankungen an den Börsen zufällig und nach den Regeln der Normalverteilung verhalten.
Diese Formal hat es – vermeintlich – geschafft diese ungewissen Schwankungen des Marktes auf eine Formel zu reduzieren.
Ich verzichte hier darauf, die Formel zu veröffentlichen, da eine genaue Herleitung sowieso den Rahmen des Artikels sprengen würde. Wer sich interessiert kann hier auf wikipedia nachlesen.
Welche Probleme sich daraus ergeben können, habe ich bereits in obigen Beispielen gezeigt. Was die Formel aber für Folgen hatte kann man hier weiterlesen:
Welche Folgen hatte die Black&Scholes Formel auf die Finanzmärkte:
Das blinde Vertrauen auf diese Formel kann verheerende Wirkungen haben. Das beste Beispiel dafür ist der große Hedgefonds den die beiden Nobelpreisträger für die Black & Scholes Formel gemeinsam mit John Meriwether im Jahre 1994 gegründet hatten: Long Term Capital Management – kurz: LTCM.
Bei den Anlagestrategien dieses Fonds wurde die neue Formel oft angewandt. Auf der einen Seite wurden Optionen die aufgrund dieser Formel zu teuer erschienen einfach verkauft, auf der anderen Seite wurden Volatilitätserwartungen bei bestimmten Märkten aufgrund dieser Formel berechnet und entsprechende Risiken eingegangen. Vier Jahre lange konnte LTCM sehr gute Renditen erzielen, zeitweise sogar über 30% im Jahr.
Der Fonds LTCM hielt im Jahr 1998 über 1,25 Billionen (das sind 1250 Milliarden) US-Dollar an Assets, dabei waren auch viele Derivate und Optionen. Das Eigenkapital betrug zu diesem Zeitpunkt nur 2,1 Milliarden USD, was einem Hebel von fast 600 entspricht bzw. einer Eigenkapitalquote von nur 0,17%.
Dann spielten die Märkte – aus Sicht von LTCM – verrückt. Es gab plötzlich Kursausschläge die mathematisch – nach eben dieser Black & Scholes Formel – nur einmal in Milliarden von Jahren passieren hätten dürfen. Also quasi seitdem das Universum existiert, hätten solche Kurssausschläge nie stattfinden dürfen.
Doch daran hielten sich die Finanzmärkte nicht: Asienkrise, Russlandkrise etc. bescherten den Märkten im Jahr 1998 eben genau diese Volatilität mit der mathematisch nicht gerechnet werden konnte, und so musste der Fonds LTCM von der amerikanischen Zentralbank FED und 11 weiteren großen Investmentbanken gerettet werden um noch stärkere Verwerfungen an den Finanzmärkten zu verhindern. Die FED musste dafür sogar den Leitzinssatz senken.
Details kann man auch hier unter wikipedia nachlesen.
Welche Vorteile kann man aus der Black & Scholes Formel ziehen?
Der wahre Wert einer Option bleibt also weiter im Dunkeln bzw. dem Gefühl und der Risikobereitschaft des Optionshändlers überlassen. Die Märkte agieren meiner Ansicht nach sicher NICHT nach Regeln die der gaußschen Normalverteilung entsprechen.
Man kann diese Formel aber dafür benutzen um die sogenannte implizite Volatilität einer Option auszurechnen, also die Erwartungen des Marktes was die Kursschwankungen angeht. Dadurch bekommt man ein Gefühl dafür, ob eine Option teuer oder billig ist. Es gibt mittlerweile sogar einige wichtige Indices, die diese erwartete – implizite – Volatilität von Optionen messen. Der wichtigste davon ist der amerkanische VIX-Index, welcher die implizite Volatilität von Optionen auf den S&P 500 Index misst. Ich habe ihn im Financeblog schon öfters erwähnt. Das Ausrechnen dieser impliziten Volatilität geht mittels der Black & Scholes Formel.
Man muss diese Formel auch nicht selbst händisch anwenden, wenn man mit Optionen handeln möchte, da die Handelssysteme das schon automatisch erledigen. Man braucht die Formel also nicht zu kennen, man sollte nur wissen welche Voraussetzungen sie annimmt, wie sie in etwa funktioniert, und dass es sehr gefährlich sein kann, sich blind auf sie zu verlassen.
Der Beitrag Derivate für Anfänger – Teil 2 – Bewertung von Optionen erschien zuerst auf Financeblog.
Latest Blogs
» SportWoche Podcast #142: Being John McEnroe
» Österreich-Depots: Stärker, Verbund nach Z...
» Börsegeschichte 3.1.: Extremes zu Porr, Ro...
» PIR-News: News zur Pierer Gruppe, Austriac...
» Nachlese: Glück für Polytec und Kapsch, Ma...
» Wiener Börse Party #812: Danke, Beate! ATX...
» Wiener Börse nach Zuckerl-Aus stärker: AT&...
» Börse-Inputs auf Spotify zu u.a. Kapsch Po...
» Börsepeople im Podcast S16/19: Ines Paupie
» Österreich-Depots: Guter Jahresstart wikif...
Michael Gredenberg

Inode-Gründer. Heute u.a. passionierter Radfahrer und Finanzautor via financeblog.at.
Weitere Blogs von Michael Gredenberg
» Apple - Wird der Apfel faul? (Michael Gred...
Apple hat letzte Woche mit der Veröffentlichung der Ergebnisse des letzten Quartals (Fisk...
» Unternehmensgründer vs Manager - welche Ak...
Einige der größten Konzerneder Welt werden heute noch von ihren Gründern geleite...
» Tesla - eine Bewertung unter neuen Gesicht...
Tesla – der innovative Elektroautohersteller aus dem Silicon Valley – hat letzte W...
» Negative Zinsen - an Aktien führt kein Weg...
Letzten Donnerstag hat die EZB mit der Senkung des Leitzinssatzes im EUR-Raum auf Null sowie der...
» Korrelation und Kausalität (Michael Greden...
Korrelation misst den Zusammenhang zwischen mehreren Ereignissen wie z.B. auch der Entwicklung v...